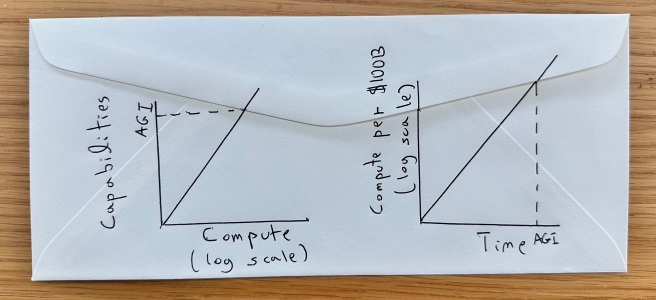
[Cross posted on lesswrong; see here for my prior writings] There have been several studies to estimate the timelines for artificial general intelligence (aka AGI). Ajeya Cotra wrote a report in 2020 (see also 2022 update) forecasting AGI based on comparisons with “biological anchors.” That is, comparing the total number of FLOPs invested in a training run or inference with … Continue reading The shape of AGI: Cartoons and back of envelope
Metaphors for AI, and why I don’t like them
Photo from National Photo Company Collection; see also (Sobel, 2017) [Cross posted in lesswrong and windows on theory see here for my prior writings]“computer, n. /kəmˈpjuːtə/. One who computes; a calculator, reckoner; specifically a person employed to make calculations in an observatory, in surveying, etc”, Oxford English Dictionary “There is no reason why mental as well as bodily labor should not … Continue reading Metaphors for AI, and why I don’t like them
The (local) unit of intelligence is FLOPs
[Crossposting again on Lesswrong and Windowsontheory, with the hope I am not overstaying my welcome in LW.] Wealth can be measured by dollars. This is not a perfect measurement: it’s hard to account for purchasing power and circumstances when comparing people across varying countries or time periods. However, within a particular place and time, one can measure … Continue reading The (local) unit of intelligence is FLOPs
GPT as an “Intelligence Forklift.”
[See my post with Edelman on AI takeover and Aaronson on AI scenarios. This is a rough, with various fine print, caveats, and other discussions missing. Cross-posted on Windows on Theory.] One challenge for considering the implications of “artificial intelligence,” especially of the “general” variety, is that we don’t have a consensus definition of intelligence. The Oxford Companion … Continue reading GPT as an “Intelligence Forklift.”
5 worlds of AI
Scott Aaronson and I wrote a post about 5 possible worlds for (the progress of) Artificial Intelligence. See Scott's blog for the post itself and discussions. The post was, of course, inspired by the classic essay on the 5 worlds of computational complexity by Russell Impagliazzo who will be turning 60 soon - Happy birthday!
Thoughts on AI safety
Last week, I gave a lecture on AI safety as part of my deep learning foundations course. In this post, I’ll try to write down a few of my thoughts on this topic. (The lecture was three hours, and this blog post will not cover all of what we discussed or all the points that … Continue reading Thoughts on AI safety
TCS for all travel grants and speaker nominations (guest post by Elena Grigorescu)
TCS for All (previously TCS Women) Spotlight Workshop at STOC 2023/Theory Fest: Travel grants and call for speaker nominations You are cordially invited to our TCS for All Spotlight Workshop! The workshop will be held on Thursday, June 22nd, 2023 (2-4pm), in Orlando, Florida, USA, as part of the 54th Symposium on Theory of Computing (STOC) and TheoryFest! The workshop … Continue reading TCS for all travel grants and speaker nominations (guest post by Elena Grigorescu)
Interview about this blog in the Bulletin of the EATCS
Luca Trevisan recently interviewed me for the Bulletin of the EATCS (see link for the full issue, including an interview with Alexandra Silva, and technical columns by Naama Ben-David, Ryan Williams, and Yuri Gurevich). With Luca's permission, I am cross-posting it here. (I added some hyperlinks to relevant documents.) Q. Boaz, thanks for taking the … Continue reading Interview about this blog in the Bulletin of the EATCS
Provable Copyright Protection for Generative Models
See arxiv link for paper by Nikhil Vyas, Sham Kakade, and me. Conditional generative models hold much promise for novel content creation. Whether it is generating a snippet of code, piece of text, or image, such models can potentially save substantial human effort and unlock new capabilities. But there is a fly in this ointment. … Continue reading Provable Copyright Protection for Generative Models
Chatting with Claude
In my previous post I discussed how large language models can be thoughts of as the hero of the movie "memento" - their long-term memory is intact but they have limited context, which can be an issue in retrieving not just facts that happened after the training, but also the relevant facts that did appear … Continue reading Chatting with Claude