In the last post we discussed some questions about discrepancy and the ‘Six Standard Deviations Suffice’ theorem stated below (without the , which is not too important, but makes for a great title):
Theorem 1 For vectors
, there exists
such that for every
,
.
In this post (second and the most technical of the three post series) we will see a proof of the above result. The theorem was proved by Spencer in 1985 using Beck’s partial coloring approach. Independently of Spencer, the result was proved by Gluskin in 1988 in a convex geometric context. Here we will review Gluskin’s proof which is quite beautiful.
Gluskin’s proof will also give us an excuse to look at some elegant (and simple to describe) results in convex geometry which may be of use elsewhere. Finally, the geometric view here will actually be useful in the next post when we discuss an algorithmic proof. Gluskin’s paper is truly remarkable and seems to reinvent several key ideas from scratch such as Sidak’s lemma, a version of Kanter’s lemma for Gaussians in convex geometry and even has the partial coloring approach implicit in it. I recommend taking a look at the paper even if it is a bit of a tough read. Much of the content in the post is based on discussions with Shachar Lovett and Oded Regev, but all mistakes are mine.
Gluskin’s proof follows the partial coloring approach with the crucial lemma proved using a volume argument. The partial coloring method was introduced by Beck in 1981 and all proofs of Theorem 1 and many other important discrepancy results in fact use this method. Here, instead of looking for a solution as in the theorem, one looks for a
solution first. This is meaningless to begin with as we can just output the all zeros vector. The main idea is to instead look for a
solution which has
support. We then recurse on the set of coordinates which are set to
. If everything goes according to plan, as we are geometrically decreasing the ambient dimension, we similarly get geometrically decreasing discrepancy bounds which we can tolerate. I won’t go into the details here, but let’s accept that it suffices to show the following:
Lemma 2 For vectors
, there exists
such that for every
,
and
.
To prove the above partial-coloring-lemma, let us first rephrase the problem in a geometric language. Let be the symmetric convex set (symmetric meaning
implies
) defined as follows for
to be chosen later:
We want to show that contains a
lattice point of large support. We show this indirectly by proving that
instead contains a lot of points from
. Gluskin does this by a clever volume argument: first show that the volume of
is large and then apply Minkowski’s theorem to show that there are many lattice points. To lower bound the first volume, Gluskin actually works in the Gaussian space.
I don’t have a clear intuitive reason for why the Gaussian distribution is better than the Lebesgue measure in this context. But if one looks at the analysis, a clear advantage is that projections behave better (when considering volumes) in the Gaussian space. For example, if we take a set like , then the Lebsgue volume of
is infinite, but if we project along the first coordinate it becomes finite. In the Gaussian case, both volumes are the same.
We next go over all the main pieces in Gluskin’s proof.
Sidak’s Lemma Suppose we have a standard Gaussian vector . Then, for any unit vector
,
has the standard normal distribution. Now, suppose we have several unit vectors
. Then, the random variables
are individually standard normals, but are correlated with one another. Sidak’s lemma (1967) says that no matter what the correlations of
‘s are, to bound the probability that none of the
‘s is too large, the “worst-behaviour” one could expect is for them to be independent. Concretely:
Lemma 3 (Sidak’s Lemma) Let
and let
be a standard Gaussian vector. Then, for all
,
The proof of the lemma is actually not too hard and an excellent exposition can be found in this paper.
The lemma is actually a very special case of a longstanding open problem called the Correlation Conjecture. Let me digress a little bit to state this beautiful question. In the above setup, let slab . Then, Sidak’s lemma says that for
,
The correlation conjecture asserts that this inequality is in fact true for all symmetric convex sets (in fact, we only need to look at ). Sidak’s lemma says the conjecture is true for slabs. It is also known to be true for ellipsoids. The statement for ellipsoids also has a discrepancy implication leading to a vector generalization of Spencer’s theorem (pointed to me by Krzysztof Oleszkiewicz). But that’s for another day.
Kanter’s Lemma The second inequality we need is a comparison inequality due to Kanter. The lemma essentially lets us lift certain relations between two distributions to their product distributions
and I think should be useful in other contexts. For instance, I recently used it in this paper in a completely different context. To state the lemma, we need the notion of peakedness of distributions.
Let be two symmetric distributions on
for some
. We say
is less peaked than
(written
) if for all symmetric convex sets
,
. Intuitively, this means that
is putting less of its mass near the origin than
(hence the term less peaked). For example,
.
Kanter’s lemma says that the peakedness relation tensorises provided we have unimodality. A univariate distribution is unimodal if the corresponding probability density function has a single maximum and no other local maxima. I won’t define what it means for a multivariate distribution to be unimodal here, but we only need the lemma for univariate distributions. See this survey for the formal definition.
Lemma 4 (Kanter’s lemma) Let
be two symmetric distributions on
such that
and let
be a unimodal distribution on
. Then, the product distributions
,
on
, satisfy
.
The proof of the lemma is not too hard, but is non-trivial in that it uses the Brunn-Minkowski’s inequality. Combining the above lemma with the not-too-hard fact that the standard Gaussian distribution is less peaked than the uniform distribution on , we get:
Minkowski’s Theorem The final piece we need is the classical Minkowski’s theorem form lattice geometry:
Theorem 6 (Minkowski’s Theorem) Let
be a symmetric convex set of Lebesgue volume more than
for an integer
. Then,
contains at least
points from the integer lattice
.
Putting Things Together We will prove the partial coloring lemma Lemma 2. The proof will be a sequence of simple implications using the above lemmas. Recall the definition of :
Our goal (Lemma 2) is equivalent to showing that contains a
point of large support.
Note that is the intersection of
slabs. Therefore, by Sidak’s lemma, for
,
where the last inequality follows from the fact that has the Gaussian distribution with standard deviation
. Therefore, if we pick
, sufficiently big then
Now, let be the uniform distribution on
. Then, by Corollary 5, and the definition of peakedness,
. Hence, the Lebesgue volume of
is at least
. Therefore, for sufficiently small
, Lebesgue volume of
. Thus, by applying Minkowski’s theorem to the symmetric convex set
we get that
has at least
lattice points.
Now, note that the only lattice points in are elements of
inside
. Therefore
has at least
points from
. By a simple counting argument at least one of these lattice points,
, must
non-zero coordinates – which is exactly what we need to prove Lemma 2!
Discussion The above argument can actually be simplified by replacing the use of Kanter’s lemma with an appropriate version of Miknowski’s theorem for Gaussian volume as done here. But I like any excuse to discuss Kanter’s lemma.
More importantly, the proof seems to be more amenable to generalization. The core of the proof really is to use Sidak’s lemma to lower bound the Gaussian volume of the convex set . Whenever you have such a statement you should even get a corresponding discrepancy statement. In particular, the matrix discrepancy conjecture from last post, essentially reduces to the following probability question:
Question Is it true that for a universal constant
, for all symmetric matrices
with
,
Acknowledgments Thanks to Shachar Lovett, Oded Regev and Nikhil Srivastava for helpful suggestions, comments, and corrections during the preparation of this post.
Very nice post!
I may be missing something, but I think Giannopoulos’s proof also gives the implication from Gaussian volume lower bounds to a partial coloring.
Let be the set of “small discrepancy fractional colorings” (the same set you define), and assume
be the set of “small discrepancy fractional colorings” (the same set you define), and assume ![\Pr_g[g \in K] > 2^{-c_1n}](https://s0.wp.com/latex.php?latex=%5CPr_g%5Bg+%5Cin+K%5D+%3E+2%5E%7B-c_1n%7D&bg=eeeeee&fg=666666&s=0&c=20201002) . Then let
. Then let  be the number of sign sequences
be the number of sign sequences  such that
such that 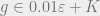 . From looking at the pdf of the standard gaussian,
. From looking at the pdf of the standard gaussian, ![\Pr[g \in 0.01\varepsilon + K] >= 2^{-c_2n}](https://s0.wp.com/latex.php?latex=%5CPr%5Bg+%5Cin+0.01%5Cvarepsilon+%2B+K%5D+%3E%3D+2%5E%7B-c_2n%7D&bg=eeeeee&fg=666666&s=0&c=20201002) for some
for some 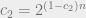 . So there must exist a point $\latex x$ which is in at least
. So there must exist a point $\latex x$ which is in at least  sets
sets  . For any two
. For any two  ,
,  , and since
, and since 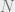 is so large, there must exist two
is so large, there must exist two  such that
such that  and
and  has large support. I chose 0.01 very conservatively, much better constants should do the job.
has large support. I chose 0.01 very conservatively, much better constants should do the job.
But Kanter’s lemma is cool in any case!
Indeed, Giannopoulos’s proof is simpler – one can view the argument you described (a typo: c_2 should be a constant) as a kind of Gaussian version of Minkowski’s theorem which by itself is a nice thing to know.
Sorry for the typo. I wish there was a way to preview comments by the way.
I could’ve been more explicit:![\Pr[g \in x + K] \geq e^{0.5\|x\|_2^2}](https://s0.wp.com/latex.php?latex=%5CPr%5Bg+%5Cin+x+%2B+K%5D+%5Cgeq+e%5E%7B0.5%5C%7Cx%5C%7C_2%5E2%7D&bg=eeeeee&fg=666666&s=0&c=20201002) for any centrally symmetric $K$ and any
for any centrally symmetric $K$ and any  , so
, so  . I guess I was really conservative with constants.
. I guess I was really conservative with constants.