Doing Theoretical Physics with Semidefinite Programming

I just came back from the Simons Foudnations annual meeting for Mathematical and Physical Sciences. Unfortunately, due to a flight delay I missed many of the talks, but the ones I did see were fascinating.

One talk in particular caught my attention: Leonardo Rastelli‘s talk on “The Superconformal Bootstrap” who discussed the work of the Simons Bootstrap collaboration. I didn’t understand much of the talk (in fact, probably less than 10 percent) but the high level tidbits I got seemed fascinating, and so am posting here some of my understanding. Most, if not all, of what is written below is probably false or inaccurate, but I hope other people that understand this more will correct me.

So, it seems one way to think of a physical theory is as being a way to predict some observables. More formally, a theory maps a point in spacetime to the observable values. In fact apparently the right way to think about this map is to map a tuple of points to the correlation between these observables, something that is known as a “correlation function”.

The traditional view is that these observables arise out of some local interactions between particles. In a computer science way, we could think of modelling spacetime by a graph G such as the d-dimensional lattice. The state of the system corresponds to some assignment of values to the vertices of G, and there is some function that maps each state to its “energy” by summing up   over the local interactions. Then the probability of obtaining a particular assignment is weighed by something exponentially small in its energy, and the predictions are obtained by sampling (or computing analytically) this distribution. Unfortunately, it seems (if I understand correctly) that there are some theories for which the physicists don’t know of (and even strongly suspect that there exists no) such local “Lagrangian” explanation for the theory. Moreover (as we can all relate to), even when such an explanation exists, computing the global predictions from the local information could be very hard.

Apparently however, if one posits certain symmetries on the theory, and particular conformal symmetry (which I believe means that the theory be scale free – the predictions are the same if we focus on a small region of space time as it would be in a large one, and is also invariant under rotations), then there are some global constraints on the form of these theories. However, figuring out what these constraints mean is not so simple, and I guess many physicists thought that even after doing all this work, probably they would not be able to derive much from these seemingly few global constraints.

However, it turns out that they can use semidefinite programming to calculate constraints on the allowed theories in “theoryspace” and in fact, using these semidefinite programs alone it might be possible to completely determine some properties of physical theories from first principles. This is not  about using optimization to analyze data in applied physics but rather doing pure theoretical physics via semidefinite programming. (In fact, if I understand correctly, these conformal theories are about idealized universes which do not precisely match our own.)

This reminds me of course of Razborov’s Flag Algebra work of using semidefinite programming to derive inequalities in combinatorics. In fact, at least to me, some of the notation used in both cases look quite similar (one of the figures below is from a talk by Lovász on flag algebras, the other is from the Simons collaboration on the superconformal bootstrap)

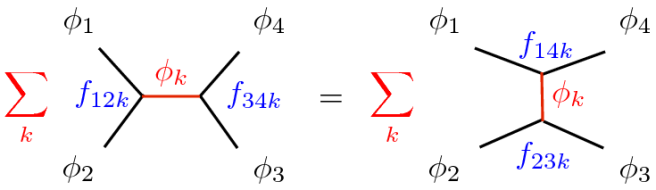
One can almost imagine an updated version of David Hilbert’s famous quote

We hear within us the perpetual call: There is the problem. Seek its solution. You can find it by semidefinite programming, for in mathematics there is no ignorabimus.

p.s.  Scott Aaronson invokes a roughly contemporaneous quote of Roosevelt in discounting critics. While I agree with both of Scott’s sentiment and the examples he mentions (except perhaps that the particular “critics” he talks about are best left alone in the dark corners of the Internet), I can’t help but thinking that he is being a little hypocritical. After all, Scott himself keeps criticizing one person who constantly strives valiantly for the American people. A person that, unlike some of his critics, was never captured by the enemy, but overcame debilitating foot spurs to achieve great skill in golf, only to make the ultimate sacrifice and restrict his playing to the weekends for the good of the nation. A person who unites Americans of all stripes, from white nationalists to businessmen who want their taxes cut.  Perhaps Scott can take some of his own medicine, and learn to appreciate greatness (and bigness) rather than criticize it.