On the Raz-Tal oracle separation of BQP and PH

By Boaz Barak and Jarosław Błasiok

[Jarek gave a great informal exposition of this paper on Friday, and I asked him to make it into a blog post. My only knowledge of the paper is from Jarek’s explanations: my main contribution to this post was to delete some details and insert some inaccuracies –Boaz.]

A recent exciting paper of Ran Raz and Avishay Tal solved a longstanding problem in quantum complexity theory: the existence of an oracle under which the class $\mathbf{BQP}$ is not contained in the polynomial hierarchy. The proof is elegant and actually not extremely complicated, and in this blog post we discuss the main idea behind it. For some of the motivation and background of this problem, see the posts of Scott Aaronson and Lance Fortnow. As is actually often the case in such relativization result, the proof does not have much to do with either $\mathbf{BQP}$ or the polynomial hierarchy. Rather at its heart is a new lower bound against the perennial “victim” of circuit lower bounds: the class $\mathbf{AC}_0$ of constant depth circuits with AND, OR and NOT gates.

Rather than thinking about a single choice of an oracle, it turns out that it’s better to think of a distribution over oracles, and (for notational convenience) as a distribution $D$ over pairs of oracles $X,Y:\{0,1\}^n \rightarrow \{ \pm 1 \}$ .
They show that:

There is a quantum algorithm that can make one quantum query to each of these oracles, and using this distinguish with advantage at least $\epsilon = 1/poly(n)$ between the case that $X$ and $Y$ are sampled from $D$ , and the case that $X$ and $Y$ are sampled from the uniform distribution. (Set $\epsilon = 1/n$ for concreteness.)
For every constant depth polynomial size circuit $C$ on $2N$ inputs (where $N = 2^n$ ), the probability that $C$ outputs $1$ on $(X,Y)$ sampled from $D$ differs by at most $\tilde{O}(\tfrac{1}{\sqrt{N}}))= \tilde{O}(2^{-n/2})$ from the probability it outputs $1$ on $(X,Y)$ sampled from the uniform distribution.

Together 1 and 2 imply the main results by standard arguments.

The distribution 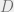$D$

The distribution $D$ they use is (a variant of) the “Forrelation” distribution proposed for this task by Aaronson. Namely, they choose $Y$ to be $\epsilon$ correlated with the Fourier transform of $X$ .

Specifically however, it is better to think about this distribution as follows:

Sample $(X,Y)$ as correlated Gaussian random variables over $\mathbb{R}^{2N}$ with the covariance matrix $\begin{pmatrix} I & H \\ H^{-1} & I \end{pmatrix}$ where $H$ is the $N\times N$ Hadamard matrix defined as $H_{x,y} = \tfrac{1}{\sqrt{N}}(-1)^{\langle x,y \rangle}$ for every $x,y \in \{0,1\}^n$ . Another way to think about this is that $X$ is a standard normal, and $Y=HX$ . Note that for any $i, j$ , $\mathbb{E} X_i Y_j = \pm \frac{1}{\sqrt{N}}$ .
Then let $D$ be the distribution over $\{ \pm 1 \}^{2N}$ that has the expectation $(\epsilon X,\epsilon Y)$ . That is, for $i,j \in \{1,\ldots,N\}$ , we choose $D_i$ as a $\pm 1$ random variable with expectation $\epsilon X_i$ and $D_{N+j}$ as a $\pm 1$ random variable with expectation $\epsilon Y_j$ . If $|X_i|$ or $|Y_j|$ are larger than $1/\epsilon$ and each coordinate is a standard Normal then we truncate them appropriately, but because we set $\epsilon=1/n$ this will only happen with probability $2^{-\Omega(n^2)}$ which we can treat as negligible and ignore this event from now on.

Distinguishing 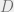$D$ from uniform is easy for quantum algorithms

The heart of the proof is in the classical part, and so we will merely sketch why this problem is easy for quantum algorithms. A Quantum Algorithm that gets query access to $X$ and $Y$ , which we think of as functions mapping $\alpha\in \{0,1\}^n$ to $\{ \pm 1\}$ can obtain the state

$\sum_{\alpha} X(\alpha) |0\rangle |\alpha \rangle + \sum_{\alpha} Y(\alpha) |1\rangle |\alpha \rangle$

The algorithm can then perform the Quantum Fourier Transform (in this case applying Hadamard to its qubits $2..n+1$ ) to change this to the state

$\sum_{\alpha} \hat{X}(\alpha) |0\rangle |\alpha \rangle + \sum_{\alpha} Y(\alpha) |1\rangle |\alpha \rangle$

But in our case, $Y$ will be $\epsilon$ correlated with $\hat{X}$ and so this can be shown to have the form

$\epsilon (|0\rangle + |1\rangle)\rho + \rho'$

where $\rho$ is some state on the last $n$ qubits.

If we now perform the Hadamard operation on the first qubit and measure it, we will be about $\epsilon$ more likely to see a zero than to see a 1. On the other hand it is not hard to show that if the input was uniform then we will see zero and one with equal probability. The advantage of $\epsilon$ can be amplified by making more queries or considering “tensored” forms of the same oracles.

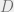$D$ is pseudorandom for AC0 circuits

We now come to the heart of the proof: showing that it is hard to distinguish $D$ from the uniform distribution for $AC_0$ circuits. One of the challenges of obtaining such an oracle separation is that the standard approach of showing such a result, which is to show that $D$ fools low degree polynomials, is not available to us. Indeed, our quantum algorithm itself is a degree 2 polyonomial in $X$ and $Y$ !

At a high level, the proof shows that AC0 circuits can be approximated (to a certain extent) by very special kind of low degree polynomials – ones that are sparse in the sense that the L1 norm of their coefficients is not much larger than the L2 norm.

Anyway, we are getting ahead of ourselves. Let $f:\{ \pm 1 \}^{2N} \rightarrow \{ \pm 1 \}$ be computable by a polynomial size constant depth $AC_0$ circuit. Our goal is to show the following result:

Main Theorem: $|\mathbb{E} f(D) - \mathbb{E} f(U) | \leq \tilde{O}(\frac{1}{\sqrt{N}})$

We will identify such a function $f$ with its multilinear extention, and hence think of $f$ as the polynomial $f(Z) = \sum_{S \subseteq [2N]} \hat{f}(S)\mathbb{E} \prod_{i\in S}Z_i$ . Note that in this notation, $\mathbb{E} f(U) = \hat{f}(\emptyset) = f(0)$ .

We start with the following simple observation: for every multilinear map $f:\mathbb{R}^{2N} \rightarrow \mathbb{R}$ , and $(X,Y) \in \mathbb{R}^{2N}$ , if we sample from a product distribution $D$ where the expectation of each coordinate matches the coordinate in $(X,Y)$ , then $\mathbb{E} f(D) = f(X,Y)$ . This means that for the purposes of analyzing the main theorem, we could just as well imagine that $D$ is sampled from the normal multivariate distribution $Z$ over $\mathbb{R}^{2N}$ with correlation matrix $\epsilon^2 \begin{pmatrix} I & H \\ H^{-1} & I \end{pmatrix}$ .

Hence the result will follow from the following result:

Main Lemma Let $Z$ be any multivariate Gaussian distribution over $\mathbb{R}^M$ such that $\mathbb{E} Z_i^2 = o( \log^{-1/2} (M/\delta))$ and $|\mathbb{E} Z_i Z_j | \leq \delta$ for $i\neq j$ . Then $Z$ is $\tilde{O}(\delta)$ pseudorandom w.r.t. multilinear polynomials computable by polynomial sized circuits of constant depth.

The $\tilde{O}$ notation hides factors poly-logarithmic in $M$ . In our case, the distribution $Z$ satisfies $\mathbb{E} Z_i^2 = \epsilon^2 = 1/n$ , and $|\mathbb{E}Z_iZ_j| \leq \tfrac{1}{\sqrt{N}}$ and so we get that $Z$ (and hence our original $D$ ) is $\tilde{O}(\tfrac{1}{\sqrt{N}})$ pseudorandom, completing the proof of the main theorem.

Note that the Main Lemma is of interest in its own right – it says that for a multivariate Gaussian to fool AC0, it is enough that the second moments sufficiently decay as long as the diagonal entries are moderately bounded away from 1. (However, for multivariate Gaussians, a bound on the second moments also implies decay of higher moments by Isserlis’ theorem.)

Proof of the Main Lemma

The Main Lemma is proved by a “Hybrid Argument”. (Related to arguments used by Chattopadhyay, Hatami, Hosseini and Lovett for constructing pseudorandom generators.) We will set $T = (M/\delta)^{10}$ . Since a sum of Gaussians is a Gaussian, for every multivariate Gaussian $Z$ , we can write

$Z = \tfrac{1}{\sqrt{T}}\sum_{i=1}^T Z^i$

where $Z^i$ is identically distributed to $Z$ .

We write $Z^{\leq i} = \tfrac{1}{\sqrt{T}}\sum_{j=1}^i Z^j$ . To prove the Main Lemma we need to show that $|\mathbb{E}f(Z^{\leq T}) - f(0)| \leq \tilde{O}(\delta)$ for every constant-depth poly-size computable multilinear $f$ . To do so we will establish the following inequality:

$| \mathbb{E} f(Z^{\leq i}+\tfrac{1}{\sqrt{T}}Z^{i+1}) - \mathbb{E} f(Z^{\leq i}) | \leq \tilde{O}(\tfrac{\delta}{T}) \;\;\;\;(*)$
for every $i=0,1,\ldots,T-1$ . (Writing $Z^{\leq 0}$ for the $0$ vector.)
We can obtain the main lemma by summing up $(*)$ over all $i=0,\ldots, T-1$ .

The main tool we will use to establish $(*)$ is the following structural result on AC0, which is again of independent interest:

L1 bound theorem: Let $f:\mathbb{R}^M \rightarrow \mathbb{R}$ be a function computable by an $\mathbf{AC}_0$ circuit of quasipolynomial size and constant depth, and let $z_0 \in [-1/2,+1/2]^M$ and $\delta<1/100$ . Then the function $g:\mathbb{R}^M \rightarrow \mathbb{R}$ defined as $g(z) = f(\delta z+z_0)-f(z_0)$ satisfies that
$\sum_{U \subseteq [M], |U|=k} |\hat{g}(U)| \leq (2 \delta)^k (\log N)^{O(k)}$ for every $k \geq 1$ .

For $z_0 = 0$ those bounds on Fourier coefficients were proven by Avishay Tal. It turns out that general case can be essentially reduced to this case by a clever random restriction.

The L1 bound theorem implies $(*)$ , by writing $g(z)=f(\tfrac{1}{\sqrt{T}}z+z_0)-f(z_0)$ for $z_0$ sampled from $Z^{\leq i}$ . (The event $z_0 \in [-1/2,+1/2]^M$ holds with high probability. It can be shown that conditioning on this event changes the relevant expectations in $(*)$ by at most an additive term that is proportional to the failure probability, which is smaller than $\frac{\delta}{T}$ .)

We can then bound the lefthand side of $(*)$ , by

$\sum_{k \geq 1}\sum_{U \subseteq [M], |U|=k} |\hat{g}(U)| \mathbb{E} \prod_{i\in U}Z_i \leq \sum_{k \geq 1}(\tfrac{2}{\sqrt{T}})^k (\log N)^{O(k)} \mathbb{E} \prod_{i\in U}Z_i$
the moment for $k=1$ vanishes. In the moments arising from $k\geq 3$ , the term $(\tfrac{1}{\sqrt{T}})^k$ makes the contribution negligible, even when we sum it over $T$ terms — by Isserlis’ theorem we mentioned above we can bound $|\mathbb{E} \prod_{i \in U} Z_i| \leq (\delta k)^k \leq T^{0.1k}$ . The only interesting term is when $k=2$ where we get exactly $\tilde{O}(\delta/T)$ as desired. (As an aside, Isserlis’ Theorem gives a way to compute the moments of any multivariate Gaussian, and has a beautiful two line proof using Taylor expansion of $\mathbb{E} \exp(\sum \lambda_i Z_i) = \exp(0.5 \mathbb{E} (\sum \lambda_i Z_i)^2)$ in the formal variables $\lambda_1,\ldots,\lambda_M$ .)

Proof of the L1 bound theorem

We now show the proof of the L1 bound theorem. We say that function $h$ is a restriction of $f$ , if $h(z) = f(r(z))$ where $r(z)_i \in \{1, -1, z_i\}$ .

Claim: For every fixed $z_0 \in [-1/2, 1/2]^M$ and multilinear $f$ there exist a random $h$ which is restriction of $f$ , such that
$g(z) = f(\delta z + z_0) = \mathbb{E}_{h} h(2 \delta z).$

Indeed, for given $z_0$ , take a variable $\tilde{z} \in \mathbb{R}^M$ , such that on each coordinate independently we have $\tilde{z}_i = 2\delta z_i$ with probability $\frac{1}{2}$ , $\tilde{z_i} = 1$ with probability $(z_0)_i/2 + \frac{1}{4}$ , and $\tilde{z}_i = -1$ otherwise. Note that $\mathbb{E} \tilde{z} = \delta z + z_0$ . Since $f$ is multilinear, and $\tilde{z}$ is independent across coordinates, we have
$g(z) = f(\delta z + z_0) = f(\mathbb{E} \tilde{z}) = \mathbb{E} f(\tilde{z}) = \mathbb{E} h(2 \delta z),$
where $h$ depending on realization of $\tilde{z}$ is a corresponding restriction of $f$ — it fixes coordinates where $\tilde{z}_i \in \{\pm 1\}$ accordingly.

Now the L1 bound theorem follows by linearity of Fourier transform: for specific $U$ we have $\hat{g}(U) = \mathbb{E}_h (2\delta)^{|U|} \hat{h}(U)$ . Every realization of $h$ as a restriction of an $\mathbf{AC}_0$ circuit is again an $\mathbf{AC}_0$ circuit (both size and depth can only decrease), hence we can apply the bounds on Fourier coeffiecients of $\mathbf{AC}_0$ circuits to $h$ , namely $\sum_{|U| = k} |\hat{h}(U)| \leq (\log N)^{O(k)}$ . Plugging those together we get
$\sum_{U \subset [M], |U| = k} |\hat{g}(U)| \leq \mathbb{E}_h \sum_{|U| = k} |\hat{h}(U)| (2\delta)^k \leq (2\delta)^k (\log N)^{O(k)}.$

which is what we needed to prove.

	James Cross on GPT as an “Intelligence…
	Thoughts on AI safet… on AI will change the world, but…
	Anonymous on An alarming trend in K-12 Math…
	Interview about this… on Men in Computer Science
	Interview about this… on The Swiss Army Knife of C…

On the Raz-Tal oracle separation of BQP and PH

The distribution $D$

Distinguishing $D$ from uniform is easy for quantum algorithms

$D$ is pseudorandom for AC0 circuits

Proof of the Main Lemma

Proof of the L1 bound theorem

Published by Boaz Barak

Leave a Reply Cancel reply

The distribution

Distinguishing from uniform is easy for quantum algorithms

is pseudorandom for AC0 circuits

Proof of the Main Lemma

Proof of the L1 bound theorem

Share this:

Like this:

Related

Published by Boaz Barak

Leave a Reply Cancel reply

The distribution $D$

Distinguishing $D$ from uniform is easy for quantum algorithms

$D$ is pseudorandom for AC0 circuits