Different areas of mathematics, and theoretical computer science, freely borrow tools and ideas from each other and these interactions, like barters, can make both parties richer. In fact it’s even better than barter: the objects being ideas, you don’t have to actually give them up in an exchange.
And so it is no surprise that differential privacy has used tools from several other fields, including complexity, cryptography, learning theory and high-dimensional geometry. Today I want to talk about a little giving back. A small interest payment, if you will. Below I will describe how differential privacy tools helped us resolve a question of Alon and Kalai.
Discrepancy
This particular instance deals with discrepancy theory, more specifically, with the Erdös Discrepancy problem (EDP)(polymath 5 being discussed here).
In 1932, Erdös conjectured:
Conjecture[Problem 9 here] For any constant , there is an
such that the following holds. For any function
, there exists an
and a
such that
For any , the sets
is a arithmetic progression containing
; we call such a set a Homogenous Arithmetic Progression (HAP). The conjecture above says that for any red blue coloring of the [n], there is some HAP which has a lot more of red than blue (or vice versa).
In modern language, this is a question about discrepancy of HAPs. So let me define discrepancy first. Let be a universe and let
denote a family of subsets of
. A coloring
of
is an assignment
. The discrepancy of a set
under the coloring is simply
; the imbalance of the set. The discrepancy of a set system under a coloring is the maximum discrepancy of any of the sets in the family. The minimum of this quantity over all colorings is then defined to be the discrepancy of the set system. We want a coloring in which all sets in
are as close to balanced as possible. In other words, if
denotes the set-element incidence matrix of the set system, then
.
Thus the conjecture says that the discrepancy of HAPs over grows with
.
This post deals with the related concept of Hereditary Discrepancy. The discrepancy can often be small by accident: even though the set system is complex enough to contain a high discrepancy set system in it, it can have discrepancy zero. The hereditary discrepancy measures the maximum discrepancy of any set system “contained” in .
Formally, given a set system , and a subset
, the restriction of
to
is another set system
, where
. If we think of the set system as a hypergraph on
, then the restriction is the induced hypergraph on
. The hereditary discrepancy
is the maximum discrepancy of any of its restrictions. In matrix language,
is simply
where the maximum is taken over all submatrices of
.
Some examples. Let denote
. A totally unimodular matrix
gives us a set system with hereditary discrepancy at most
. An arbitrary collection of
sets has discrepancy at most
. Note that a random coloring will give discrepancy about
. In a famous paper, Spencershowed the
upper bound, and Bansal and recently Lovett and Meka gave constructive versions of this result.
Privacy
Given a vector , and
–
matrix
, consider the problem of outputting a vector
such that
is small, and yet the distribution of
isdifferentially private, i.e. for
and
that are close the distributions of the corresponding
‘s are close. If you are a regular reader of this blog, you must be no stranger to differential privacy. For the purposes of this post, a mechanism
satisfies differential privacy if for any
such that
, and any (measurable)
:
Thus if are close in
, the distributions
are close in
.
Researchers have studied the question of designing good mechanisms for specific matrices . Here by good, we mean that the expected value of the error say
, or
is as small as possible. It is natural to also prove lower bounds on the error needed to answer specific queries of interest.
A particular set of queries of interest is the following. The coordinates of the vector are associated with the hypercube
. Think of
binary attributes people may have, and for
,
denotes the number of people with
as their attribute vector. For each subcube, defined by fixing
of the
bits, we look at the counting query corresponding to that subcube: i.e.
. This corresponds to dot product with a vector
with
being one on the subcube, and zero elsewhere. Thus we may want to ask how many people have a
in the first and second attribute, and a
in the fourth. Consider the matrix
defined by all the possible subcube queries.
Subcubes defined by fixing bits are
-juntas to some people, contingency table queries to others. These queries being important from a statistical point of view, Kasiviswanathan, Rudelson, Smith and Ullman showed lower bounds on the amount of error any differentrially private mechanism must add, for any constant
. When
is
, their work suggests that one should get a lower bound that is
.
The connection
So what has discrepancy got to do with privacy? Muthukrishnan and Nikolov showed that if has large hereditary discrepancy, then any differentially private mechanism must incur large expected squared error. In fact, one can go back and check that nearly all known lower bounds for differentially private mechanism are really hereditary discrepancy lower bounds in disguise. Thus there is a deep connection between
and the minimum achievable error for
.
For the EDP, it is natural to ask how large the hereditary discrepancy is. Alon and Kalai show that it is and at most
. They also showed that for constant
, it is possible to delete an
fraction of the integers in
, so that the remaining set system has hereditary discrepancy at most polylogarithmic in
. Gil guessed that the truth is closer to the lower bound.
Alex Nikolov and I managed to show that this is not the case. Since hereditary discrepancy is, well, hereditary, a lower bound on the hereditary discrepancy of a submatrix is also a lower bound on the hereditary discrepancy of whole matrix. In the EDP matrix on , we will first find our subcubes-juntas-contingency-tables matrix
above as a submatrix; one for which
is
. Having done that, it would remain to prove a lower bound for
itself.
The first step is done as follows: associate each dimension with
th and the
th prime. A point
in the hypercube is naturally associated with the integer
. A subcube query can be specified by a vector
:
is set to the appropriate
–
value for the coordinates that we fix, and
for the unconstrained coordinates. We can associate a subcube
with the integer
. It is easy to see that
is in the subcube corresponding to
if and only if
divides
. Thus if we restrict ourselves to the integers
and HAPs corresponding to
, we have found a submatrix of the EDP matrix that looks exactly like our contingency tables matrix
. Thus the hereditary discrepancy of the EDP matrix is at least as large as that of this submatrix that we found.
Lower bounds for private mechanisms for can be derived in many ways. For constant
, the results of Kasiviswanathan et al. referred to above suffice and it is likely that they can be pushed to get the
lower bounds we are shooting for. A very different approach of extracting from weak random sources also implies such a lower bound. It is likely that from these, one could get a lower bound on
of the kind we need.
However, given what we know about , we can in fact remove the privacy scaffolding and get a simpler direct proof of the lower bound of
on
, and can write a proof of the lower bound without any mention of privacy. This implies that the hereditary discrepancy for the EDP is at least
, which matches the upper bound up to a constant in the exponent. A brief note with the proof is here.
Of course the EDP itself is wide open. Head on here to help settle the conjecture.
Many thanks to Alex Nikolov for his contribution to the content and the writing of this post.
Great post. Reminds me of a talk Avi once gave titled something like “why it’s worthwhile sitting in talks in different fields.” I should add that sometimes fields don’t only borrow ideas but also borrow the researchers from other fields. So beware guys … 🙂
Where did you define EDP?
My bad. EDP is the Erd\”os discrepancy problem that we started the post with. Now fixed.
Great! Just saw the post.
Very nice post! I have always thought about constructing DP lower bounds as equivalent to showing the existence of large packings around the optimal value. For example, our sample complexity bounds for learning in [1] and statistics [2] are all based on this concept of packings. Do you know if there’s a formal relationship between the two concepts?
[1] Sample Complexity Bounds for Differentially Private Learning
Kamalika Chaudhuri and Daniel Hsu, COLT 2011
[2] Convergence Rates for Differentially Private Statistical Estimation
Kamalika Chaudhuri and Daniel Hsu, ICML 2012
Thanks for the pointers.
For (eps,0)-differential privacy, pretty much all lower bounds I know of are based on packing arguments. For linear queries, Moritz and I showed[1] that this is tight up to a polylog factor. We can go a little further than packing based lower bounds[2] by”adding up” packing-based lower bounds over orthogonal subspaces. It is a good question if packing based LBs are nearly tight in some more general setting.
For (eps,delta)-differential privacy, the picture is quite different. Packing based lower bounds only apply when delta is really small, and do not apply for say polynomially small delta. In fact, you can sometimes get (eps,1/poly(n))-DP mechanisms with accuracy significantly better than the packing based lower bounds for (eps,0) [3].
So in most settings, for proving non-trivial lower bounds of (eps,delta), one must go beyond packings. Many of the lower bounds go via lower bounds for some variant of blatant non-privacy. As this post mentions, these are often lower bounds on discrepancy, or on the smallest eigenvalue of an associated matrix.
[1] Hardt and Talwar, The Geometry of Differential Privacy. http://arxiv.org/abs/0907.3754
[2] Bhaskara et al. Unconditional Differentially Private Mechanisms for linear queries. http://www.cs.princeton.edu/~bhaskara/files/privacy.pdf
[3] Anindya De, Lower bounds on Differential Privacy, http://arxiv.org/abs/1107.2183
Another paper from the same period that uses the packing technique:
A. Beimel, S. P. Kasiviswanathan, and K. Nissim. Bounds on the Sample Complexity for Private Learning and Private Data Release. In the Seventh Theory of Cryptography Conference, 2010. http://www.cs.bgu.ac.il/~beimel/Papers/BKN.pdf
The references [2] and [3] were flipped. Just fixed that.
Also, just to clarify, I did not mean to suggest that [1] introduced packing arguments. There are earlier papers with a packing argument, and certainly people in the community knew of it independently well before it appeared in print. What I find surprising is that in many settings, it is tight or nearly tight for (eps,0). Our failure to come up with more clever lower bounding techniques is, in many cases, not our fault. 🙂
The definition of EDP given above is not quite correct. The problem is to bound all partial sums of the function along HAPs, not just the sums that go all the way up to .
.
(Indeed, the conjecture as stated is trivially false: one can take and define
and define 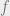 by
by 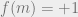 if
if  and
and  if
if  .)
.)
(The definition given in the paper is correct …)
Thanks for the correction. Now fixed.
Great post.
Are the following known? Any references or pointers would be welcome.
1. Fix $n$. Let $A_k$ be the $C_k^n \times 2^n$ matrix encoding subcube queries with $k$ of $n$ input variables fixed. What is the (plain, nonhereditary) discrepancy of $A$? In the 2 norm? In the infinity norm?
2. What about including all $k$ from 1 to $n$? Hence what is the discrepancy of all subcube queries?
For subcubes of co-dimension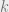 , the discrepancy is 0 if
, the discrepancy is 0 if 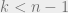 and 1 otherwise (in the infinity norm, $lates \sqrt{n}$ in
and 1 otherwise (in the infinity norm, $lates \sqrt{n}$ in 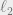 ). For all subcubes, it is 1 in infinity norm and
). For all subcubes, it is 1 in infinity norm and  in
in 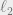 .
.
All of these are achieved by the parity coloring: the color of is
is  . It is easy to see this has discrepancy 0 for any subcube of dimension greater than 0 (i.e. any subcube which is not a vertex).
. It is easy to see this has discrepancy 0 for any subcube of dimension greater than 0 (i.e. any subcube which is not a vertex).
Thanks!